大多数深度学习算法都涉及到优化,优化是指改变x来最大化或最小化某个函数f(x)。
1. 学习和纯优化有什么不同
用于深度模型训练的优化算法与传统的优化有几方面是不同的:机器学习通常是间接作用的,比如间接地优化P,一般通过降低损失函数来提高P;
经验风险最小化
我们将最小化平均训练误差的过程称为经验风险最小化(Empirical Risk Minimization),这种情况下,机器学习仍然和传统的直接优化很相似。我们不是直接最优化风险,而是最优化经验风险,希望也能够同时显著降低风险。然而,经验风险最小化容易导致过拟合,在深度学习中我们很少使用它。
代理损失函数和提前终止
有时,真正的损失函数(比如分类误差)并不能被高效地优化。这种情况下,我们通常会优化代理损失函数。代理损失函数作为原目标的代理,还具备一些优点。在某些情况下,代理损失函数比原函数学到的更多。一般的优化和训练算法的优化有一个重要的不同:训练算法一般不会停止在局部极小点。这么做是为了防止过拟合,一般会使用提前终止机制。与纯优化相比,提前终止时代理损失函数仍有很大的导数,而纯优化终止时导数比较小。
批量算法和小批量算法
机器学习算法和一般优化算法不同的一点是:机器学习算法的目标函数通常可以分解为训练样本上的求和。机器学习中的优化算法在计算参数的每一次更新时通常仅使用整个代价函数中一部分项来估计代价函数的期望值。使用整个训练集的优化算法被称为批量或确定性梯度算法,因为它们会在一个大批量中同时处理所有样本。每次只使用单个样本的优化算法有时被称为随机或者在线算法。术语“在线”通常是指从连续产生样本的数据流中抽取样本的情况,而不是从一个固定大小的训练集中遍历多次采样的情况。小批量的大小通常用以下几个因素决定:
- 更大的批量会计算精度更高的梯度估计,但是回报却是小于线性。
- 极小批量通常难以充分利用多核架构,这促使我们使用一些绝对最小批量。
- 如果批量处理中的所有样本可以并行地处理,那么内存消耗和批量大小会成正比。
- 在某些硬件上使用特定大小的数组时,运行时间会更少。尤其是在使用GPU时,通常使用2的幂数作为批量大小可以获得更少的运行时间。
- 可能由于小批量在学习过程中加入了噪声,它们会有一些正则化效果。泛化误差通常在批量大小为1时最好。
小批量是随机抽取的,这一点很重要。一般地,我们会将样本顺序随机打乱,然后一组组小批量样本连续读取。
2. 神经网络优化中的挑战
传统的机器学习会小心设计目标函数和约束,以确保优化问题是凸的,从而避免一般优化问题的复杂度。在训练神经网络时,我们肯定会碰到非凸的情况。即便是凸优化,也可能会碰到其他问题。
病态
病态问题一般是指在神经网络训练过程中,随机梯度下降会被“卡”在某些情况,此时即使很小的更新步长也会增加损失函数。牛顿法在解决带有病态条件的Hessian矩阵的凸优化问题时,是一个非常优秀的工具。
局部极小值
由于模型可辨识性问题,神经网络中会存在多个等效的局部极小值。一方面神经网络中会存在多个局部极小值,另一方面每个局部极小值的求解代价是不同的。有可能一个等效的局部极小值,它的代价更大。我们无法去辨识哪个代价更大。
PS:模型可辨识性:一个模型只能由唯一确定的参数所确定,不存在其他参数来等效确定。
高原、鞍点和其他平坦区域
对于很多高维非凸函数而言,相比局部极小值,鞍点存在的可能性更大。在低维空间中,局部极小值很普遍。在更高维空间中,局部极小值点很罕见,而鞍点却很常见。对于牛顿法而言,鞍点显然是一个问题。梯度下降旨在朝“下坡”移动,而非明确寻找临界点。而牛顿法的目标是寻求梯度为0的点。如果没有适当修改,牛顿法就会跳进一个鞍点。
悬崖和梯度爆炸
多层神经网络通常存在像悬崖一样的斜率较大区域,这是因为几个较大的权重相乘导致的。遇到这种悬崖结构时,梯度更新会很大程度地改变参数值,可能会使大量已完成的优化工作成为无用功。因此,我们通常选择完全跳过这类悬崖结构,常用的方法是启发式梯度截断来避免其严重的后果。其基本思想是:因为梯度并没有说明最佳不畅,只是说明无限小区域内的最佳方向,所以当传统的梯度下降算法提议更新很大一步时,启发式梯度截断就会干涉来减小步长。从而使其不太可能走出梯度近似为最陡下降方向的悬崖区。悬崖结构在循环神经网络的损失函数中很常见,因为它涉及到很多个因子的相乘。
长期依赖
当计算图变得极深时,神经网络优化算法会面临的另一个难题就是长期依赖问题:由于变深的结构使模型丧失了学习到先前信息的能力,让优化变得极其困难。同时会造成梯度消失与梯度爆炸问题。梯度消失使得我们难以知道参数朝哪个方向移动来改进损失函数;而梯度爆炸会使得学习不稳定。在循环网络中,一般使用相同权重矩阵来避免这个问题。
3. 基本算法
随机梯度下降
基本思想:将数据中抽取m个小批量样本,通过计算它们梯度均值,我们可以得到梯度的无偏估计。SGD算法中的一个关键参数学习率。在实践中,推荐使用随着时间的推移逐渐降低学习率的策略。对于大数据集,SGD只需非常少量样本计算梯度从而实现初始快速更新,远远超过了其缓慢的渐近收敛。

动量
虽然随机梯度下降仍然是非常受欢迎的优化方法,但其学习过程有时会很慢。动量方法旨在加速学习,特别是处理高曲率、小但一致的梯度,或是带噪声的梯度。动量算法积累了之前梯度指数级衰减的移动平均,并且继续沿该方向移动。
从形式上看,动量算法引入了变量v充当速度角色,它即代表参数的移动方向,又代表速率。速度被设为负梯度的指数衰减平均。梯度下降算法基于每个梯度简单地更新一步,而使用动量算法的牛顿方案则使用该力改变粒子的速度。我们可以将粒子视作在冰面上滑行的冰球。每当它沿着表面最陡的部分下降时,它会累积继续在该方向上滑行的速度,直到其开始向上滑动为止。
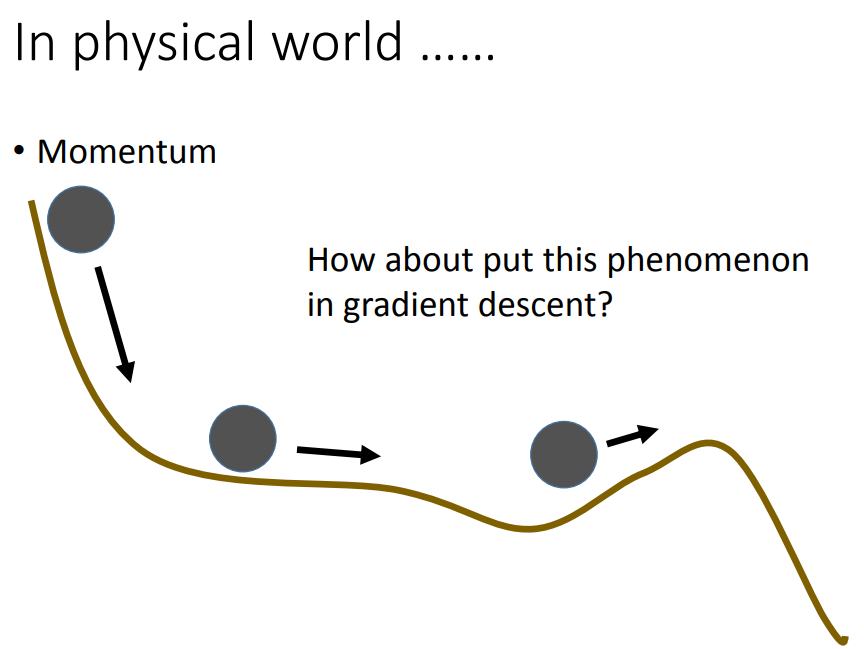
形象地,我们可以将损失函数看出山的高度,然后我们将一个小球从这个山上滚下来。小球的速度会越来越快,使得小球可以越过山腰上的沟壑,有机会快速到达谷底。并且为了防止小球速度过快,我们会设置一个超参,该参数相当于物理中的阻尼系数。

Nesterov动量
Nesterov动量和标准动量之间的区别体现在梯度计算上,Nesterov动量中,梯度计算发生在施加当前速度之后。因此,Nesterov动量可以解释为往标准方法中添加了一个校正因子。

如上图所示,我们可以对比一下Nesterov动量法和标准动量法区别。动量法首先计算当前的梯度值(小蓝色向量),然后在更新的积累向量(大蓝色向量)方向前进一大步。但 NAG 法则首先(试探性地)在之前积累的梯度方向(棕色向量)前进一大步,再根据当前地情况修正,以得到最终的前进方向(绿色向量)。这种基于预测的更新方法,使我们避免过快地前进,并提高了算法地响应能力(responsiveness),大大改进了 RNN 在一些任务上的表现。
4. 参数初始化策略
深度模型的训练算法通常是迭代的,所以需要指定一些开始迭代的初始点,这些初始点会影响算法是否收敛。并且当算法收敛时,初始点还可以影响其收敛的速度,以及是否收敛到一个代价高或低的点。现在的初始化策略是简单的、启发式的。我们对于初始点如何影响泛化的理解相当原始的,几乎没有提供如何选择初始点的任何指导。
到目前为止,唯一确知的特性是初始参数需要在不同单元间“破坏对称性”:如果两个隐藏层单元有着相同的激活函数以及相同的输入,那么它们必须使用不同的初始参数。通常情况下,我们可以为每个单元的偏置设置启发式挑选的常数,仅随机初始化权重。我们经常 对权重的选取随机取自高斯或均匀分布中的值。
关于初始化网络,正则化和优化有着不同的观点。优化观点建议权重 尽可能成功地传播信息,而正则化希望其小一点。优化算法倾向于最终参数应接近初始参数。
设置偏置的方法必须和设置权重的方法协调。设置偏置为0在大多数初始化方案中是可行的,但也存在一些设置为非0 的情况:
- 如果偏置是作为输出单元,那么初始化偏置以获取正确的输出边缘统计通常是有利的。我们假设初始权重足够小,该单元的输出仅由偏置决定。这说明设置偏置为应用于训练集上输出边缘统计的激活函数的逆。
- 有时,我们会选择偏置来避免初始化引起太大饱和。
5. 自适应学习率算法
学习率会对模型的性能有显著的影响,Delta-bar-delta算法是一个早期的在训练时适应模型参数各自学习率的启发式方法。其基本思想:如果损失对于某个给定模型参数的偏导保持相同的符号,那么学习率应该增加。如果对于该参数的偏导变化了符号,那么学习率应减小。这种方法只能应用于全批量优化中,最近提出一些增量(或基于小批量)的算法来自适应模型参数的学习率。
AdaGrad
此算法独立地适应模型所有参数的学习率,缩放每个参数反比于其所有梯度历史平方值总和的平方根。具有损失最大的偏导的参数相应地有一个快速下降的学习率,而具有小偏导的参数在学习率上有相对较小的下降。然而在实践中,发现从训练开始时积累梯度平方会导致有效学习率过早和过量的减小。
RMSProp
此算法修改AdaGrad以在非凸设定下效果更好,改变梯度积累为指数加权的移动平均。RMSProp使用指数衰减平均以丢失遥远过去的历史,使其能够在找到凸碗状结构后快速收敛。
Adam
Adam利用了AdaGrad和RMSProp在稀疏数据上的优点,对初始化的偏差修正也让Adam表现的更好。很多deep learning的优化问题都用Adam。
6. 二阶近似方法
牛顿法
牛顿法是基于二阶泰勒级数展开在某地$\theta_0$附件来近似$J(\theta)$的优化方法,其忽略了高阶导数。对于局部的二次函数,用Hession矩阵的逆来重新调整梯度,牛顿法会直接跳到极小值。如果目标函数是凸的但非二次的(有高阶项),该更新将是迭代的。牛顿法要保证Hession矩阵是正定才能使其是有效的,并且牛顿法还受限于其显著的计算负担。这就导致只有参数很少的网络才能在实际中用牛顿法训练。
共轭梯度
共轭梯度是一种通过迭代下降的共轭方向以有效避免Hession矩阵求逆计算的方法,其中在于梯度相关的方向上使用了线搜索。该方法在二次碗型目标中是一个相当低效的来回往复,锯齿形模式。这是因为每个由梯度给定的线搜索方向,都保证正交于上一个线搜索方向。
在共轭梯度法中,我们寻求一个和先前线搜索方向共轭的搜索方向,即它不会撤销该方向上的进展。
BFGS
Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法具有牛顿法的一些优点,但没有牛顿法的计算负担。在这方面,BFGS和CG很像。然而,BFGS使用了一个更直接的方法近似牛顿更新,使用矩阵M近似逆,迭代地低秩更新精度以更好的近似Hession的逆。
与共轭梯度法相似,BFGS算法迭代一系列线搜索,其方向含二阶信息。与共轭梯度不同的是,该方法的成功并不严重依赖于线搜索寻找该方向上和真正极小值很近的一点,这样的话,BFGS花费较少的时间改进每个线搜索。另一方面,BFGS算法必须存储Hession逆矩阵M,使得BFGS不适用于大多数具有百万级参数的现代深度学习模型。
存储受限的BFGS(L-BFGS)
通过避免存储完整的Hession逆近似M,BFGS算法的存储代价可以显著降低。
1
本文内容摘取自《Deep Learning》,部分内容有所修改
