XGBoost是数据挖掘类竞赛中经常使用的一大利器,它帮助选手在Kaggle、阿里天池大数据比赛等比赛取得了很好的成绩。XGBoost被很多人使用,但很少人知道其原理,前几天看了一下陈天奇大神的论文有了更多的理解。XGBoost是基于GBDT(Gradient Boosting Decision Tree) 改进而来的,本文将对XGBoost算法原理进行介绍,主要通过以下几个部分进行介绍:boosted trees、目标函数正则化、节点切分算法。
注: 本文假设读者理解回归树算法、泰勒公式、梯度下降法和牛顿法
1. Boosted trees
Boosted trees是一种集成方法,Boosting算法是一种加法模型(additive training),定义如下:
![]()
这里K是树的棵数,f(x)是函数空间中的一个函数:![]()
q(x)表示将样本x分到了某个叶子节点上,w是叶子节点的分数(leaf score)
下面通过一个具体的例子来说明:预测一个人是否喜欢电脑游戏,下图表明小男孩更喜欢打游戏。
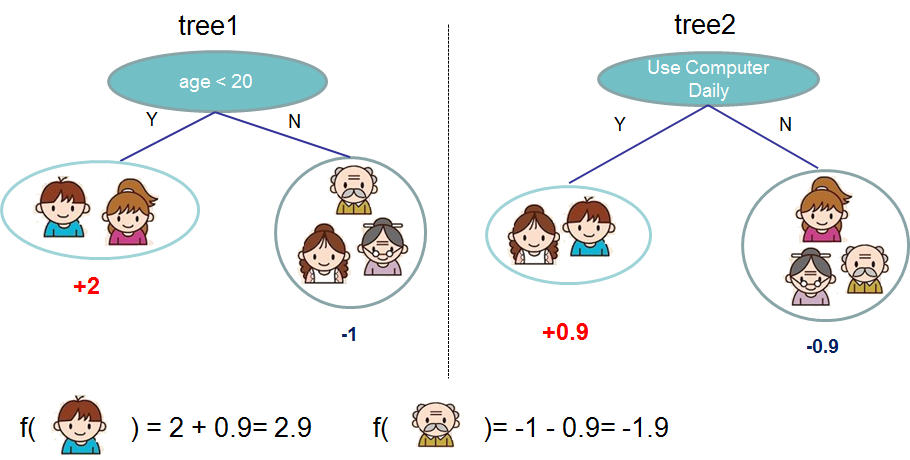
2. 目标函数正则化
XGBoost使用的目标函数如下:
![]()
我们可以看出XGBoost在GBDT的误差函数基础上加入了L1和L2正则项,其中Loss函数可以是平方损失或逻辑损失,T代表叶子节点数,w代表叶子节点的分数。加入正则项的好处是防止过拟合,这个好处是由两方面体现的:一是预剪枝,因为正则项中有限定叶子节点数;二是正则项里leaf scroe的L2模平方的系数,对leaf scroe做了平滑。
接下来我们对目标函数进行目标函数的求解:
![]()
该目标函数表示:第i样本的第t次迭代误差函数,后面的推导基于上式。这种学习方式已经从函数空间转到了函数空间:
![]()
下面对目标函数进行泰勒公式二级展开、化简:
![]()
![]()
![]()
如果确定了树的结构,为了使目标函数最小,可以令其导数为0,解得每个叶节点的最优预测分数为:
![]()
代入目标函数,解得最小损失为:
![]()
3. 节点切分算法
我们已经确定了损失函数,以及最优解,接下来我们需要缺点树的结构,即如何选出最优分裂节点。我们可以参照决策树算法:ID3选择信息增益为切分准则,C4.5选择信息增益率为切分准则。XGBoost基本思想是和决策树一致的:贪心法枚举所有节点,计算各个节点分裂前后的信息增益,选出信息增益最大的。下面是XGBoost信息增益的定义:
![]()
XGBoost提供了两种切分算法:精确贪心算法和近似算法
精确贪心算法: 在所有特征上暴力枚举所有可能的切分点,算法如下:
![]()
近似算法: 其基本思想:首先根据特征的统计分布(分位数)选出候选切分点;然后对于连续属性特征,根据候选切分点进行离散化;最后会从这些候选切分点中选出最优的。近似算法提出了两种版本:global variant和local variant. global variant在树初始化时就确定了候选切分点;local variant是在每次节点分裂后重新选出候选点。论文中的实验表明:在同等精度下,相对于global variant, local variant需要的候选切分点更少。近似算法如下:
![]()
近似算法举例:三分位数
![]()
注: 近似算法中使用到了分位数,关于分位数的选取,论文提出了一种算法Weighted Quantile Sketch 。XGBoost不是按照样本个数进行分位,而是以二阶导数为权重。
![]()
Q: 为什么使用hi加权?
A: 比较直观的解释是因为目标函数可以化简为如下形式:
4. 其他
在实际工作中,大多数输入是稀疏的。造成稀疏的原因有很多种,比如:缺失值、one-hot编码等。因此,论文提出为树中的节点设置一个默认方向来应对稀疏输入。论文实验表明稀疏感知算法 要比传统方法快50倍,算法如下:
![]()
下面通过例子具体说明:
![]()
注: 红色路径代表默认方向
Shrinkage: 可以理解为学习率,算法每次迭代后会乘这个系数;
列采样: 降低过拟合,论文实验表明列采样比行采样效果好。
